Durant 2000 anys molts matemàtics van dedicar el seu temps i els seus esforços a completar amb nous teoremes aquesta gran construcció que és la geometria d'Euclides. Alguns d'ells van tractar de reduir el nombre inicial de postulats, ja que es pensava que el 5º postulat podia demostrar-se a partir dels altres quatre. És a dir, volien convertir el 5º axioma en teorema, en aquest cas bastaria acceptar els quatre primers axiomes i prendre'ls com a punt de partida per a obtenir finalment la mateixa geometria.
De la mateixa forma que un arquitecte calcula els fonaments precisos perquè la torre que desitja construir siga el més esvelta possible, així fan els matemàtics quan cerquen els axiomes més convenients per a la seua teoria i, quants menys axiomes utilitzen, més elegant serà el resultat final.
Per a convertir el 5º postulat en un teorema, era necessari obtenir una demostració, i a açò es van dedicar sense èxit molts matemàtics al llarg de diversos segles. Va ser a principis del segle XIX quan tres matemàtics, Lobachevski en Russia, Gauss a Alemanya i Bolyai a Hongria, van donar amb un resultat inesperat que va llançar una nova llum sobre aquesta qüestió. Van treballar independentment uns d'uns altres en l'elaboració de models geomètrics que mantenien els quatre primers postulats d'Euclides alhora que negaven el cinquè. Esperaven que una geometria en la qual es negara que "per un punt exterior a una recta pasa una única paral·lela", seria una geometria incoherent i plena de contradiccions.
Existeixen diverses propostes i tipus de Geometries no Euclidianas, alguns exemples són: Geometria Hiperbòlica, Geometria Esfèrica. Les Geometries no Euclidianas són molt importants per al desenvolupament de la Física, específicament en l'Astronomia. També és fonamental per a conèixer l'Univers matemàtic, ampliar l'Horitzó de dues i tres dimensions a un possible Univers de n dimensions.
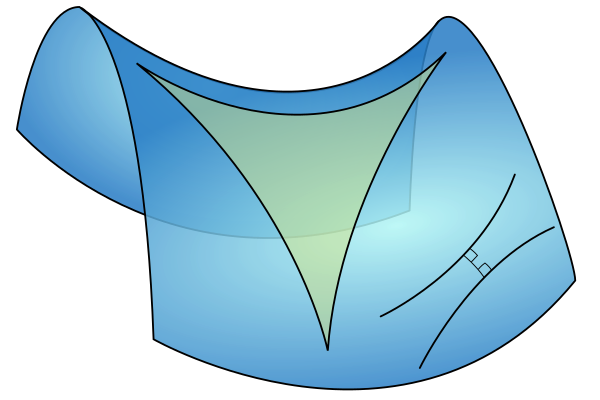 |
| Un triangle en una superfície amb forma de una sella de muntar (un paraboloide hiperbòlic), i dues rectes paral·leles divergents. Font |



